Units of Wavelength
(click on equations to view enlarged)
For many applications, particularly when dealing in the infrared region of the spectrum, the preferred spectral unit is wavelength in μm, λ = 106 c/ν. We can deduce the spectral radiance per μm, Lλ, from (1) by noting that
|
|
|
With this, and substituting ν = 106 c/λ into (1), the spectral radiance per μm is:
(7)
To find the wavelength of the peak, we set the derivative to zero:
Letting x = 106hc/λkT
(8)
The peak value, found by substituting (8) into (7), is
(9)
As we did above with spectral units of Hz, we can derive these radiometric quantities in terms of photons per second. Dividing (7) by the energy of a photon, 106 hc/λ, gives the spectral photon radiance,
. (10)
The wavelength where this peaks is found by differentiating:
. (11)
The peak spectral photon radiance is
. (12)
Lλ and LλP are shown in Fig. 2. Note that as with units of Hz, the spectral radiance and spectral photon radiance have different behaviors, and distinctly different temperature dependences.
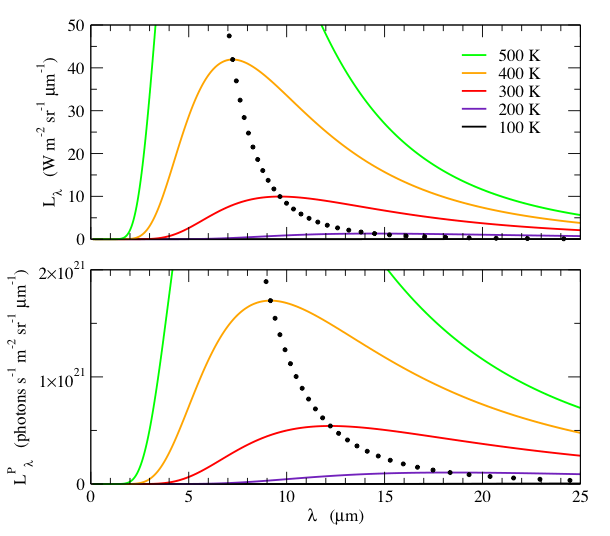
Fig. 2: Spectral radiance, Lλ, (top) and the spectral photon radiance, LλP, (bottom) as a function of wavelength, λ, for various temperatures. The small black dots indicate the wavelength and value of the peak, at 10 K temperature intervals. Note that Lλ and LλP have different wavelength dependences. Although the peak wavelength is inversely proportional to T for both quantities, LλP peaks at a longer wavelength than Lλ. Furthermore, the peak value of Lλ increases as T 5, whereas the peak value of LλP increases as T 4.