Blackbody Calculator

The Planck Blackbody Formula in Units of Frequency

It can be shown[1] that the power emitted per unit projected area of a blackbody at temperature T, into a unit solid angle, in frequency interval ν to ν +dν, is

                                                                            (1)

where h is Planck’s constant (6.6260693×10⁻³⁴   W s²) ,  

            c is the speed of light (2.99792458×10⁸  m s^-1)  and

            k is Boltzmann’s constant (1.380658×10⁻²³  J K^-1) .

This is the Planck blackbody formula (in one of many forms).  The quantity L_ν is referred to as the spectral radiance.  The frequency of the maximum spectral radiance is found by setting the derivative with respect to ν equal to zero:

This gives the transcendental equation  3(1 - e ^-x) = x,  where x = hν/kT .  Evaluating this numerically yields x = a₃ ≈ 2.82143937212, so

                                                           .                                                 (2)

(We use the subscript 3 to refer to the coefficient in the transcendental equation, other versions of which we will encounter).  Substituting this in (1) gives

                                                              (3)

Many devices and systems respond in proportion to the number of incident photons, and it is useful to express radiometric quantities in terms of photons per second rather than watts.  Dividing the spectral radiance L_ν (Eq. 1) by the energy of a photon, hν, gives the spectral photon radiance

                                     .                           (4)

The peak of L_ν^P occurs when

This gives the transcendental equation 2(1 - e^-x) = x, where x = hν/kT, with solution x = a₂ ≈ 1.59362426004.  The peak spectral photon radiance thus occurs at frequency

                                                           .                                                 (5)

Note that the peak of L_ν^P occurs at a lower frequency than L_ν.  The peak value of L_ν^P is found by substituting (5) into (4):

                                                    (6)

Both L_ν and L_ν^P are shown in Fig. 1, for several temperatures.

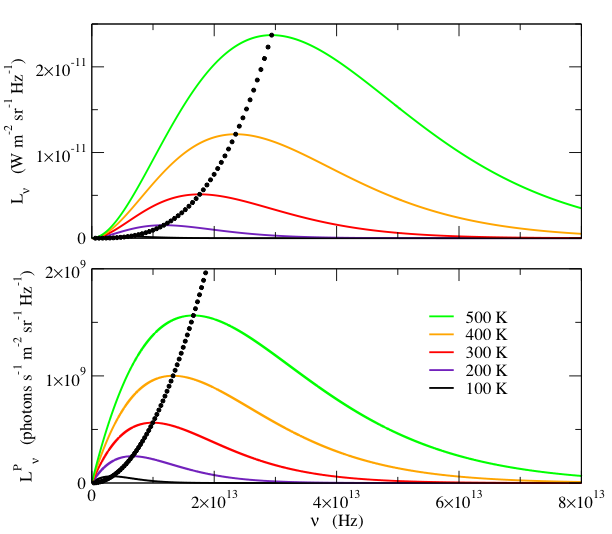
Fig. 1-Spectral radiance, L_ν, (top) and the spectral photon radiance, L_ν^P, (bottom) as a function of frequency, ν, for various temperatures.  The small black dots indicate the frequency and value of the peak, at 10 K temperature intervals.  Note that L_ν and L_ν^P have different frequency dependences.  Although the peak frequency is proportional to T for both quantities, L_ν peaks at a higher frequency than L_ν^P.  Furthermore, the peak value of L_ν increases as T ³, whereas the peak value of L_ν^P increases as T ².